Lately I've been playing around with graphics programming, and a need came up for a piece of code to perform triangulation of a set of points. Triangulation means you connect nearby points by lines, making triangles, so that every point is the vertex of one or more triangles.

Triangulating a set of points well turns out to be a bit of a complex problem. Even the definition of "well" is somewhat debatable, but typically the best triangulation is called a Delaunay Triangulation. In such a triangulation it is guaranteed that every triangle is as "circular" as it can be, and not unnecessarily thin and spindly. The definition of this kind of triangulation demands that the circle formed by the 3 points of every triangle does not contain any other points from the set of points we're dealing with.

Note that for any three points, as long as they are not in a straight line, one can construct a circle that runs through all the points. If the points are sort of equal distance apart you get a small circle. If the points are nearly in a line, you get a really big circle. A Delaunay Triangulation will break up any triangle that is so spindly that the circle that goes through the triangle's points is big enough to enclose other points. Wikipedia is a great source for more information on triangulation, I'm just mentioning it because it was the subject that got me headed on the subject this essay is about.

Now as I said I was interested in an algorithm for doing a triangulation. Along that pursuit naturally I could find working code examples on the web that I can incorporate, but I am sometimes a do-it-yourself type of person. Moreover other people's code is frequently buggy, incomplete, or spaghetti, and I liken using other people's code to wearing someone else's underwear. Who knows where it's been. Anyway I was interested in developing an algorithm for doing the triangulation of a set of points, and I was thinking about the Convex Hull.

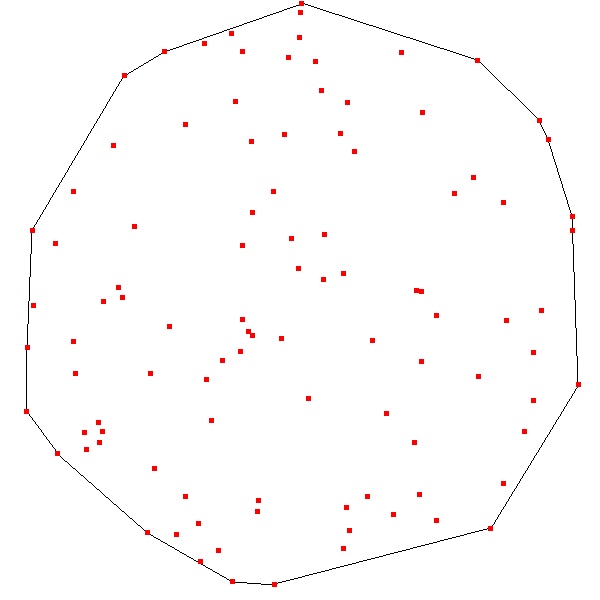The Convex Hull of a set of points is the outermost "rim" of points such that when neighboring points are connected together there are no concaveties, or indentations, and there are no other points from the set outside the hull. If your set of points were in a plane, and you were to bring a line in of any arbitrary orientation from infinity to contact the set of points, the first point it contacts from any direction will lie on the convex hull of the set. See the image on the left, that shows a line drawn along the points of the convex hull for a random set of 100 points.

Finding the convex hull is a tricky problem in its own right, there are a number of algorithms for finding those points. I'm only interested in the two dimensional case, but the convex hull can exist in any number of dimensions. For a set of points in three dimensions the convex hull is the set of points first touched by bringing an infinite plane into contact with the set from infinity. You get 2 dimensional flat surfaces on the convext hull, not lines, in this case.

Now I had thought that the convex hull might be helpful in finding the Delaunay Triangulation of a set of points. Why did I think this? First of all it is obvious that in any triangulation of points the points on the convex hull must be joined as parts of triangles. That is because there are no points outside the convex hull that can be used to make triangles, so neighboring points on the convex hull must be members of the same triangle. There is probably a nice formal proof for this but it's just something I accept intuitively.

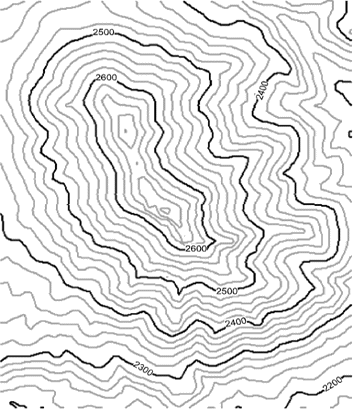The second reason I thought it might be helpful is that around 30 years ago, in the 1970's, my dad had mentioned some work he had done in writing a program to draw contour maps. Contour maps are maps where lines are drawn that indicate constant altitude. They go around mountains and canyons, "sideways" along the contour. They don't go up or down slopes, they go across the slope, or the gradient, of the local terrain. My dad had mentioned that the problem of drawing contour maps is a bit tricky. The image on the right is an example of a contour map.

As he explained it, his program would start with a set of points in two dimensions. For each point there is a height, or altitude, value. Suppose one point is representing 1000 feet, and a nearby one is representing 1500 feet, and there are no points in between. If you want to draw a contour line that shows 1200 feet, you can simply assume that these two points you have to work with are connected by a line. And so you can just locate the point that is 40% of the way along the line between the 1000 foot point and the 1500 foot point. Whatever the actual terrain is, you only have so much data to work with, so you have to interpolate between points to guess at where the contour lines are.

Now knowing where that 1200 foot contour line crosses the line between the 1000 foot point and the 1500 foot point, you have some useful information. If you have a third point nearby you can perhaps interpolate between that point and the original two and find other points where the 1200 foot contour line crosses. Now within the triangle formed by these three points you can connect the points that are known to cross 1200 feet, and you've just drawn part of the 1200 foot contour line for this set of points.

My dad said the problem would be made very easy if you could triangulate the set of points you're starting with. Once the triangles are formed, you can always interpolate between the points of every triangle to find all the contour lines that cross this triangle. There is probably some proof that if you can find a Delaunay Triangulation of a set of points the quality of the resultant contour map will be as high as it possibly can -- you will have made the best possible use of the information you have to work with. For any region in the map you're always drawing on the closest data points to find your contour lines. So if there is a region of very high sampling (dense collection of points) you'll have accurate contour lines, and if there is a region with low density of sampled points, you'll have rough, jagged contour lines. Meaning the quality degrades nicely depending on the quality of your sample. This is always nice.

Long story short, when my dad was talking about the contour problem and about how useful it would be to triangulate the points, he mentioned that he had never managed to actually do it. Meaning implement a triangulation algorithm. He ended up "fitting the points to a grid," which is something I never fully understood. I was a kid around 10 years old, I had no trouble visualizing the triangulation, I never really understood what he meant by fitting the points to a grid. How can you move points around that are locked in place? I never understood it. Anyway he said in the effort of trying to come up with an algorithm for doing the triangulation, they considered making use of the convex hull. As I recall he had said that maybe if you could find the convex hull you could then find the next innermost convex hull, and make triangles between these two hulls, and the problem might be simplified somewhat.

So all my life this has sort of been a thought that has come back to me from time to time. Maybe the convex hull would be useful in doing a triangulation of a set of points. So lately in some programming I've been doing, as I said, I've had a use for a piece of code that triangulates points, so I had a reason to go investigate this possibility. So I looked on Wikipedia and I found a discussion of the convex hull, and I read a bit about some of the approaches to finding the points on the hull. I found a mention of a Graham scan which looked perfectly straightforward. In this approach you start by finding the bottom most point (lowest Y value). Then you order all the points based on the angle they make with the horizontal and this point.

As an example, suppose you're on the lowest point. You have a rotating gun turret. You start by facing exactly right (along the positive X axis). Then you start looking for other points in the set. You know you won't find any points on your right side, because you're standing on the bottom most point. Now every point you're staring straight at, you put in your list of points. Then you slowly turn the gun to your left, always adding points to your list as soon as you "see them". So you end up with a list of points that is ordered based on the angle they were discovered at. This is a necessary first step for performing the Graham Scan. See the animating gif image on the left, it illustrates the step by step Graham scan algorithm. Note the very dim line from the pivot point on the bottom to each point as it is being added to the list -- this line is like the line of site of the turret. See how it always turns to the left.

Now what you do is you start going through your newly sorted list, one point at a time. As you go along, you start adding points to another list you are building up. Whenever you have at least three points in the list, you can examine the last 3 points you've added. Now here is the trick. The Graham scan wants it such that your three points will only "turn" in one direction. In this case you want the points in your second list to only "turn" to the left. That means you're going around your set of points, with the group of points on your left hand side. Now as long as you're only turning to the left with each new point you're adding to your second list, you can be sure you are moving along the convex hull of the set. But once you make a right turn, there is a problem. That right turn you just added now forms a concavety, or depression, in your set of points. That means your set is no longer a convex hull -- because it is no longer convex. Something is wrong! So you have to fix the problem. It turns out what you do is you just throw away the middle point of the last three in your second list that you're building up. By making that right turn, you have discovered that an interior point is not part of the convex hull. So you simply discard it from your list.

Great! So all you do is continue stepping through your list of points, always only taking left turns, and every time you take a right turn you discard the 2nd to last point in your list. Now when you come to the end of your original list of points, you know your job is done, and the second list of points only contains the points of the convex hull. Mission accomplished!

So after reading this description on Wikipedia, I was enthusiastic. I went ahead and implemented the algorithm in a piece of code. It worked fine, as expected. So now I had a piece of code that located the convex hull of a set of points. But remember my original goal was to triangulate the points, and using the convex hull was just a possible way of assisting in that original goal. Rather than go back to the triangulation problem, I wanted to play with the convex hull some more. So I wondered if it might be useful to find the next convex hull. Meaning if you start with a set of points and you find the convex hull, suppose you take all those points away and then find the next innermost convex hull. What might that look like? Suppose you keep doing it, so you end up with a collection of closed figures, each being the unique convex hull of the remaining set of points. Maybe this would look kind of neat.

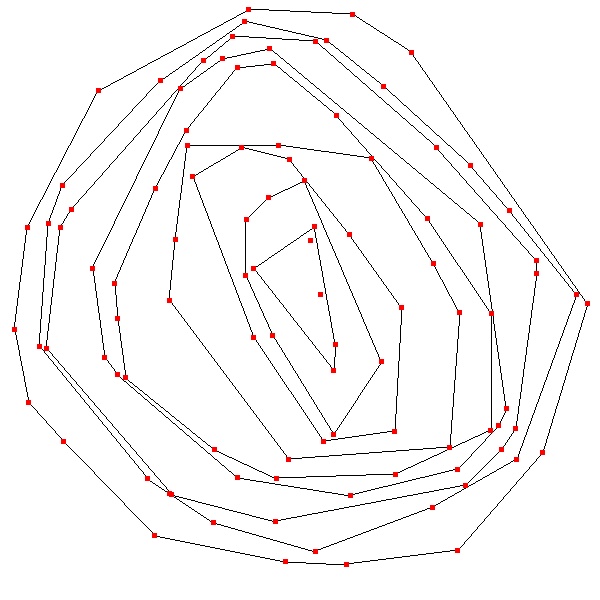So I modified my program to do this and display the convex hulls all the way down until there are no more points left. Now inside the innermost convex hull there are either 0, 1 or 2 points remaining. There can't be any more, because if there were 3 or more points, one could construct another convex hull (that would look like a triangle perhaps). So in the end you're left with 0, 1 or 2 points inside the innermost convex hull.

Having done this and looked at the results for sets containing a lot of points, I was discouraged. The convex hulls looked pretty cool, but it was clear having the convex hull would be of absolutely no use whatsoever in triangulating the set of points. Take a look at the image on the left. This is an example of all the convex hulls for a set of 100 points. Notice the two leftover points buried deep in the inner most hull. Orphaned, as it were. Nevermind the points that seem to touch the lines of the next outer convex hull, that is just a limit of the pixel resolution of the image. If you could zoom in enough you'd see a gap between each convex hull and the next one out.

The problem with the convex hulls is that the whole reason for using it in the first place is to know which points ought to be connected together in the final "best" triangulation. However it is clear there are cases where points are so close together they ought to be connected, but there is a convex hull lying in between that would have to be "cut" in order for that to happen. So even though the outer convex hull might be useful, the interior ones don't seem to help at all in the triangulation problem.

Now, having played with the convex hull problem a bit, I was having fun with it. It occured to me that Grahams scan method required sorting the list of points first, based on the angle they make relative to the bottom most point and the X axis (the direction of the "turret"). Sorting by the computer is always an O(n log n) proposition. That means it is costly in terms of computing power. Specifically, if you want to sort a lot of things, it takes a lot of processing time, and maybe you don't have infinite computing time to work with (say if you want real time interaction with the program as it's doing its thing, like in a video game). So sorting is expensive.

With Graham's scan, each time you find a convex hull you need to sort the entire set of points. It occured to me that you might be able to get by only doing the sort once. I got the idea that instead of sorting the points based on the bottom point, you chose an arbitrary point inside the points themselves, say the "average" of all the points together. Sort of the center of mass of all the points. That's easy to compute, all you do is just add up all the X coordinates and divide the sum by the total number of points, and you do the same for all the Y coordinates. This point will be interior to the group of points. One could probably prove that it must lie inside the convex hull, but I took it on faith that it would.

So instead of sorting all the points based on the angle of the bottom point, what about using the angle of the center of mass point with all the other points? It's as if the turret is stuck in the midst of all the points and it is turning around at them all. Could the Graham scan be modified to work with this new approach? The answer is yes. You still go through all your points, throwing out any that would require a "right" turn, but the problem is at the beginning you start at some arbitrary point that is not necessarily on the convex hull itself. It can be buried inside. So it becomes necessary to fix up this problem. What you do is after you've gone through the entire list of points once, you start back at the beginning again, passing the same points through the mechanism that already went through. This has the effect of getting rid of the "buried" internal points you don't want anyway. You stop once you've reached a point in your list that is still a left turn, as is the point following it.

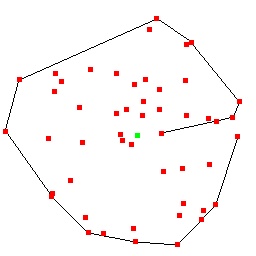
The image at the left illustrates this approach. The green point is the "center" and all other points are ordered based on their direction from this point. You see the start of the convex hull list begin at a point to the right, and work its way to the outside of the set, then proceed on outside. Then we arrive at the last point in the list, and it is clear there are some bad internal points we shouldn't have in our list. As I said, we just keep going a bit, checking the points at the start of the list, and we will quickly get rid of the ones we don't want, and we'll have the correct convex hull list.

Great! So what next? Well, after removing those points from the list, we can then start a new scan based on the remaining points. After all, they're still sorted based on their angle with respect to the center point. So all we have to do is scan through the list again and we get a new convex hull! Great!

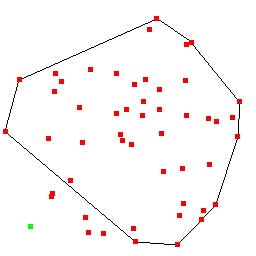Anyway it works for a while, until we get into a situation where the pivot point is outside the convext hull of the remaining points. Then the approach breaks down, and you end up getting a partial convex hull, with some of the points outside. See the image to the left. The green pivot point is in the lower left, clearly outside the convex hull. Doh! That means if we use Graham's scan, we have to keep sorting the points each time we want to find the next convex hull.

I thought about the situation a bit, and a new idea hit me. Suppose I don't sort the points based on angle -- suppose instead, I just do a simple sort based on Y, from lowest to highest. Now if I scan through the list, I can at least find half of the convex hull, say the points on the right hand side. Wait! Then I can simply reverse direction through the list and get the other half, and I end up right at the start of my list.

Moreover, after taking the convex hull points away that I just identified, the remaining points are still ordered from lowest to highest. Removing elements from a sorted list leaves the remaining elements still in order. So I can keep scanning back and forth through the list, each time identifying a new convex hull. Fantastic! So I never have to pay the O(n log n) sorting price except the first time.

Now, as I was working on implementing this, it occured to me that it might be cool if instead of identifying successive convex hulls, one inside the next, I instead just make a list of all the points in a spiral, ending up in the inside. After I got the idea I had to implement it. I call it the Convex Rind. I think of the rind of an apple peel, where you just keep cutting until you have nothing of the apple left except a long thin strip which you could roll back up into the original apple.

See the image at right, it illustrates the concept of the convex rind. You're always stepping along, taking the left turn, throwing away any points that would force you to make a right turn, and eventually you come to the end of your list (whether you're traversing it in order or in reverse order) and then you know every point still in your list can be excluded from the original list. So you keep scanning through the original list until there are no more points left, and you now have a nice single list of points, all ordered in a perfect convex spiral.

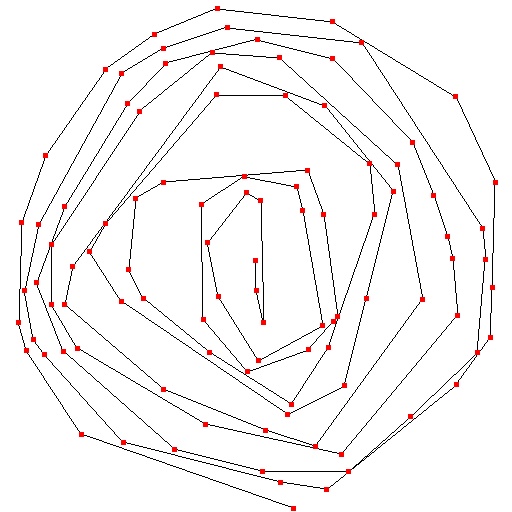
	On the left here is an example of the convex rind with 100 points.
	On the left is an example with 1000 points, and I got rid of the red point markers as they were making it too busy. Both these last two images are right-hand, in the sense that the convex rind rotates from outside to inside turning right. The other examples shown have always been left handed.

Now one thing occured to me the convex rind might be useful for. If you have a need for finding all the nested convex hulls, you can find them very easily if you already have the convex rind. What you do is start with the first point in the rind, and remember it. Then you follow along the rind in order. You will find your original point is always on the same "side" as each line segment that forms the convex rind. In the above two images, the first point lies to the "right" of each successive segment of the rind.

Now this continues, as you follow around the rind, until you've looped around once. Then you're back to your original point, only a little bit inside because, after all, you're spiralling in. Notice that your original first point is now left of the last line segment you just traversed. Aha! That must mean I left the outermost convex hull. So all you do is go back to the point just before the first "inside" point, and break the connection to the first inside point. Instead, you connect that point to the first point, and you've now made your complete outermost convex hull.

You now have a new first point of your remaining convex rind, and you start over again. This way you keep discoving successive convex hulls, until there are not enough points left to form a triangle.

I hope you enjoyed this discussion of the convex rind. I probably didn't invent the concept, but I like the name anyway. I certainly discovered it independently. It might be useful for something. It seems kind of cool to me at least.

I don't know why I keep adding this image. I can only imagine the untold misery it has already caused... SYMBOL OF DEATH! SACRED SOUTH AMERICAN INDIAN SYMBOL, WHEN GAZED UPON, CAUSES DEATH WITHIN THE YEAR! Too bad if you looked.

Access count (e^i)